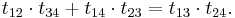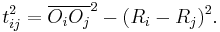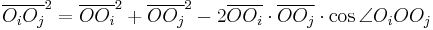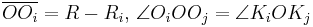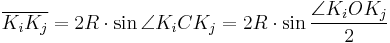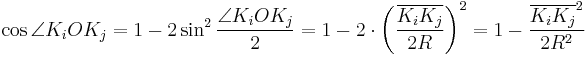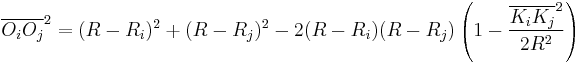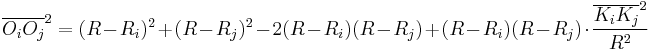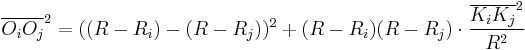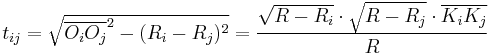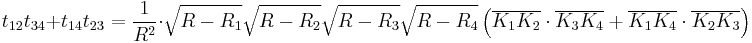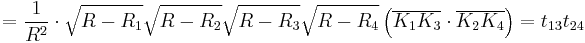Casey's theorem
In mathematics, Casey's theorem, also known as the generalized Ptolemy's theorem, is a theorem in Euclidean geometry named after the Irish mathematician John Casey.
Contents |
Formulation of the theorem
Let 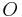 be a circle of radius
be a circle of radius 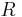 . Let
. Let 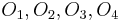 be (in that order) four non-intersecting circles that lie inside
be (in that order) four non-intersecting circles that lie inside 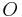 and tangent to it. Denote by
and tangent to it. Denote by 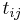 the length of the exterior common tangent of the circles
the length of the exterior common tangent of the circles 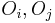 . Then[1]:
. Then[1]:
Note that in the degenerate case, where all four circles reduce to points, this is exactly Ptolemy's theorem.
Proof
The following proof is due[2] to Zacharias[3]. Denote the radius of circle 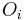 by
by 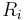 and its tangency point with the circle
and its tangency point with the circle 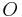 by
by 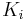 . We will use the notation
. We will use the notation 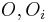 for the centers of the circles. Note that from Pythagorean theorem,
for the centers of the circles. Note that from Pythagorean theorem,
We will try to express this length in terms of the points 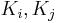 . By the law of cosines in triangle
. By the law of cosines in triangle 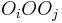 ,
,
Since the circles 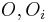 tangent to each other:
tangent to each other:
Let 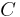 be a point on the circle
be a point on the circle 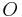 . According to the law of sines in triangle
. According to the law of sines in triangle 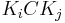 :
:
Therefore,
and substituting these in the formula above:
And finally, the length we seek is
We can now evaluate the left hand side, with the help of the original Ptolemy's theorem applied to the inscribed quadrilateral 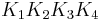 :
:
Q.E.D.
Further generalizations
It can be seen that the four circles need not lie inside the big circle. In fact, they may be tangent to it from the outside as well. In that case, the following change should be made[4]:
If 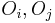 are both tangent from the same side of
are both tangent from the same side of 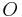 (both in or both out),
(both in or both out), 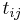 is the length of the exterior common tangent.
is the length of the exterior common tangent.
If 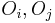 are tangent from different sides of
are tangent from different sides of 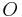 (one in and one out),
(one in and one out), 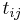 is the length of the interior common tangent.
is the length of the interior common tangent.
It is also worth noting that the converse of this statement is also true[4]. That is, if equality holds, the circles are tangent.
Applications
Casey's theorem and its converse can be used to prove a variety of statements in Euclidean geometry.
For example, the shortest known proof[1] of Feuerbach's theorem uses the converse theorem.
References
- ^ a b Casey, J. (1866), Math. Proc. R. Ir. Acad. 9: 396.
- ^ Bottema, O. (1944), Hoofdstukken uit de Elementaire Meetkunde, (translation by Reinie Erné as Topics in Elementary Geometry, Springer 2008, of the second extended edition published by Epsilon-Uitgaven 1987).
- ^ Zacharias, M. (1942), Jahresber. Deutch. Math.-Verein. 52.
- ^ a b Johnson, Roger A. (1929), Modern Geometry, Houghton Mifflin, Boston (republished facsimile by Dover 1960, 2007 as Advanced Euclidean Geometry).